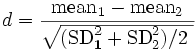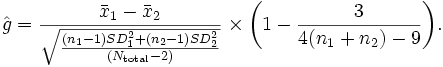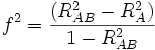Эффективность

Эффективность является измеряемой величиной, равной отношению двух переменных. В научных экспериментах довольно часто необходимо определить не только наличие эффекта эксперимента, но также определить его величину, размер. В некоторых ситуациях, величина такого эффекта, его размер, количественный показатель важны для принятия правильных решений. Вычисление величины эффективности является частой практикой мета-аналитических исследований и представляет собой выжимку, итог исследования в определенной области.

Краткая сводка

Концепция определения величины эффективности отражена даже в повседневной речи. Например, реклама часто гласит, что программа по снижению веса поможет избавиться от 30 фунтов. В данном случае, 30 фунтов – это заявленная величина эффективности. В другом случае, школьная программа поможет ученику добиться повышения его знаний и, как следствие, повышение его оценки на один балл. Такое повышение оценки вполне может служить величиной эффективности данной программы.

Еще одним примером может служить следующая ситуация. Допустим, вы никогда раньше не сталкивались с людьми как с биологическим видом, и вдруг оказались в Англии. Возникает вопрос: сколько времени у вас займет на понимание того, что в среднем мужчины здесь выше женщин? Ответом на вопрос будет величина эффекта, производимого разницей между ростом мужчин и женщин. Чем больше эффект, производимый такой разницей, тем быстрее вы поймете, что мужчины выше женщин. А если разница в росте совсем небольшая, тогда вам придется оценить и сопоставить длину тела огромного количества мужчин и женщин для того, чтобы понять, что в среднем мужчины выше. Ниже приведена иллюстрация этого примера.

В статистике вывода, величина эффективности равна величине статистически значимой разницы. Величины эффекта, наряду с N и критической альфа, определяют степень в тестировании статистической гипотезы. В мета-анализе, величины эффекта используются как количественные величины, которые могут быть вычислены в результате различных исследований и затем сведены в единый аналитический процесс.

Типы

Коррелят Пирсона r

Коррелят Пирсона r – один из основных и широко используемых величин эффекта. Его можно использовать в случаях, когда сведения идут непрерывным потоком или являются бинарными. В данном случае, коррелят Пирсона r является самой гибкой величиной эффекта. Это первая серьезная попытка оценить величину эффекта, которая была сделана Карлом Пирсоном. r может меняться в диапазоне от -1 до 1, где -1 означает полностью отрицательное отношение, а 1 – полностью положительное отношение. Величина его в 0 показывает, что между переменными нет никакой разницы в значении. Кохен (1988, 1992) дает прикладную градацию данной величины эффекта: маленькая эффективность =0,1; средняя эффективность =0,3; высокая эффективность =0,5.

Другим коэффициентом эффективности между двумя переменными является квадрат r, часто встречающийся под названием «коэффициент детерминации». Данный коэффициент показывает пропорциональность колебаний величин, наблюдаемых у двух переменных, и колеблется в пределах от 0 до 1. Например, r2 =0,21 будет говорить о том, что переменные обладают 21-процентным колебанием.

Коэффициент Кохена d

Коэффициент Кохена d является подходящим для применения в контексте t-тестов в отношении средних величин. d равен разнице между двумя средними величинами, поделенной на среднеквадратическое отклонение выборки для данных средних величин. Таким образом, в ситуации, когда оба образца равны,



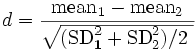
где mean_i and SD_i являются средней величиной и среднеквадратическим отклонением в группе i, i=1,2.

Разные ученые по-разному предлагают трактовать результирующее значение коэффициента, однако наиболее приемлемой представляется трактовка Кохена (1992): 0,2 – небольшой эффект, 0,5 – средний эффект, 0,8 – высокая эффективность.

Таким образом, при рассмотрении еще раз примера с попаданием в Англию, и после наблюдения за ростом мужчин и женщин, мы приходим к следующему выводу (данные взяты из британского исследования роста 2436 мужчин и 3311 женщин 2004 года):

• Мужчины: Средняя величина роста = 1750 мм; среднеквадратическое отклонение = 89.93 мм
• Женщины: Средняя величина роста = 1612 мм; среднеквадратическое отклонение = 69.05 мм

Таким образом, эффект будет равен (используя коэффициент Кохена) 1,72 ( используя 95-процентный доверительный интервал – 1,66-1,78). Данная величина весьма большая, поэтому вам не доставит никакого труда заметить ощутимую разницу между ростом мужчин и женщин в Англии.
Однако следует сказать о следующем. В определенных случаях есть смысл использовать среднеквадратическое отклонение выборки, а в других – пользоваться одним из набора среднеквадратических отклонений (например, долечебное среднеквадратическое отклонение в терапевтических исследованиях). Так или иначе, имейте в виду, что объем выборки, как и разница в выборках, в вычислении не играют никакой роли. Все вышесказанное высказал Хеджез.

Коэффициент Хеджеза ĝ

Хеджез и Олкин (1985) заметили, что возможна корректировка, уточнение величины эффективности при обращении внимания на объем выборки. Коэффициент Кохена d имеет слабое место – он зависит от величины знаменателя в уравнении. И если одно среднеквадратичное отклонение больше другого, тогда знаменатель увеличивается в сторону большего отклонения, что влечет за собой замедление роста величины эффективности. Возникает вопрос – а почему бы не ориентироваться на большее отклонение? Коэффициент Хеджеза ĝ включает в расчеты объем выборки, вычисляя знаменатель, который принимает во внимание в данном случае объемы выборки соответствующих среднеквадратических отклонений, а также производит необходимые изменения в величине общего эффекта. Формула для вычисления Коэффициент Хеджеза ĝ (используется в некоторых программах, таких как Effect Size Generator):



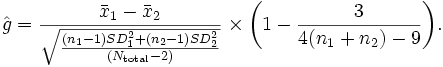
В случае с обсуждавшимся примером приезда в Англию, коэффициент Хеджеза ĝ
и, следовательно, величина эффективности будет равняться 1,76 (используя 95-процентный доверительный интервал – 1,70-1,82). Обратите внимание на то, что большой объем выборки соответствующим образом повлиял на величину эффективности, и как она отличается от такой же, но полученной при помощи метода Кохена. И если бы объем выборки составлял лишь 90 мужчин и 80 женщин, коэффициент Хеджеза ĝ показал бы более скромную величину эффективности в 1,70 (используя 95-процентный доверительный интервал – 1,35-2,05).

Коэффициент Кохена f²

Данный метод измерения величины эффективности применяется в контексте F-тестирования для множественной корреляции или множественной регрессии. Измерение величины эффективности для множественной регрессии с помощью данного метода определяется формулой:



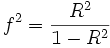
где R² – квадрат множественного коррелята.

Измерение величины эффективности для иерархичной множественной регрессии с помощью данного метода определяется формулой:



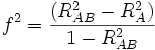
где – R²_A изменение, внесенное одной или несколькими самостоятельными переменными A, а - R²_AB комбинированное изменение, внесенное A и другой (одной или несколькими) переменными B.
Обычно величина, вычисленная с помощью данного метода, имеет следующие градации:
малая эффективность – 0,02
средняя эффективность – 0,15
высокая эффективность – 0,35
(Cohen, 1988)

Коэффициент вероятности

Коэффициент случайности является еще одним показателем величины эффективности. Данный метод пригоден для использования в том случае, когда обе переменные являются бинарными. Рассмотрим следующий пример, касающийся правописания. В контрольной группе, два учащихся сдают зачет повторно, таким образом, вероятность сдачи зачета равна 2 к 1 (2/1=2). В другой группе, 6 учащихся сдают тот же зачет, то есть вероятность сдачи равна 6 к одному (или 6/1=6). Величину эффективности можно вычислить, таким образом, беря во внимание тот факт, что вероятность сдачи зачета во второй группе в 3 раза выше (так как 6/2=3). Таким образом, коэффициент вероятности равен 3. Однако, не следует путать данный результат с полученным с помощью метода вычисления коэффициента Кохена d (который также равен 3). Это разные понятия.